- 이번에는 푸리에 급수에 대해 공부해보겠습니다.
- 이를 증명하고 어떤식으로 사용되는지 말씀드리도록 하겠습니다.
- 푸리에 급수를 알기 위해선 복소함수 및 오일러 공식을 알고오면 좋습니다!
푸리에 급수
우선 가장중요한 사실은 "모든 주기함수는 푸리에 급수로 표현이 가능하다" 입니다.

위 푸리에 급수 그림이 가장 좋은 설명일것입니다. 그 이유는 단순한 4가지 주기를 가진 함수들의 합이 새로운 input 주기 함수로 나타나는것이죠. 이게 핵심입니다. (추후 이를 이용해 분해하여 압축센싱이나 다양한 기법사용) 여기서 주의할점은 무조건 주기 함수에서만 가능하다는점 입니다.
푸리에 급수 수식 의미

위 수식을 보면서 이해해보도록 하겠습니다. $f(t)$는 우리의 input 함수라고 생각하시면 됩니다. $T$는 주기인데 보통 frequency(주파수) = 1/T 로 표현 됩니다. $C_n$은 계수인데 푸리에 급수에서 어떻게 이 값을 나타내는지 추후에 증명하도록 하겠습니다.
푸리에 급수는 각기 다른 주파수(frequency)를 가진 정현파 함수/신호(Sinusoidal Function/Signal)의 합입니다. 여기서 $w = 2\pi/T$ 로서 $w$ 를 각주파수로 정의하여 오일러 공식을 통해 대입하면 아래와 같은 식 1 으로 나타나게됩니다.
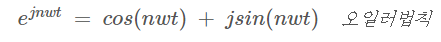

식1은 결국 $Cn$의 푸리에 계수에 곱과 나머지 cos 및 sin인 간단한 주기함수를 통해 모든 주기함수를 표현 할 수 있다 라고 얘기 할 수 있습니다!
푸리에 계수 구하기
마지막으로 푸리에 계수를 구해보겠습니다. 푸리에 계수를 구하기 위해 직교성을 활용하여 증명하도록 하겠습니다.

위에 사진을 보게되면 내적의 의미를 뜻하는데 복소수에서 내적은 컨쥬게이트 즉 $z^* * z$가 내적이라 할 수 있습니다.
$$ z = a+bi, z^* = a-bi 이기에 z^* * z = a^2 + b^2$$
위 식처럼 결국 우리는 $(a,b)^T*(a,b)$ 를 하여 내적을 하였다고 말 할 수 있습니다.
이러한 내적을 활용하여 수식을 전개한것인데 우선 위에 식을 쭉 따라가면서 어려운건 없을겁니다. 그렇게 되면 아래와 같은 최종 식이 나오게됩니다. 또한 n=q 아니면 모든값은 0이 되기때문에 n=q 일때 조건만 고려해주어 계산하면 됩니다!




