- 오늘은 코시 리만 방정식을 증명해보겠습니다.
- 어떤식으로 코시리만 방정식이 풀이되는지 예제도 함께 풀어보겠습니다.
우선 저희는 코시 리만방정식을 왜 필요로 하냐가 중요할것입니다. 중요한 이유는 복소평면 상에서 어떤 특정 함수 $f(z)$에 대해 미분이 가능한지를 알고 싶어 이 방정식을 사용하는것입니다. 이에 대해 증명 해보도록 하겠습니다.
정의
$z = x+iy$ 인 공간에서 $f(z) = u(x,y) + iv(x,y)$ 가 연속이고 미분가능 하다면 u,v는 아래의 식을 만족합니다.
$$ u_x = v_y , u_y = -v_x $$
즉 f(z)가 정의역 D에서 해석적(analytic)이라면 D의 모든 점에서 f(z)의 편도함수가 존재하고 코시-리만방정식을 만족합니다.
증명

그림 1 에서 복소함수는 어느 방향으로 Δz 를 잡더라도 미분계수가 존재할 때 미분가능합니다. 이에 대해 자세히 설명하도록 하겠습니다. 우선 저희는 실함수에서의 미분가능성에 대해 생각해봐야 합니다. 실함수에서 미분가능 조건은 다음과 같이 두개입니다.
- 미분하고자 하는 점에서 함수가 연속이다.
- 미분계수가 존재하여 좌미분계수와 우미분계수가 일치한다.
이 두가지이고 만약에 두가지 조건이 만족하지 않는 다면 아래 그림 2 와 같이 미분 불가능할것입니다.

그럼 이제 다시 복소 평면으로 돌아오면 여기서 복소함수는 $f(z) = u(x,y) + iv(x,y)$ 이고 이는 정의역 자체가 2차원 복소 평면이기에 어느 방향에서 오든 그림 3 처럼 미분이 가능해야 미분가능하다고 할 수 있습니다.
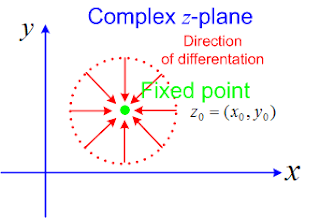
저 그림 3 에서 $\Delta z$는 어느방향에서든 올 수 있는 값입니다. 이유는 벡터의 크기라고 생각하시면 될것같습니다.(이에 대해 저도 자세히는 잘모르겠습니다.) 그럼에도 제 생각을 말씀드리면 여러방향에서 오는 $\Delta z$ 크기는 위의 그림 3처럼 모두 목표점인 $z_0 = (x_0,y_0)$ 에 대해 $z - \Delta z$ 는 원을 그리며 표현이 될것입니다. 즉 복소평면에서 미분가능하기 위해선 저 모든 방향에 대해 만족해야 한다는것이죠.
그렇기에 그림1 에서 경로 1,2에 대해 생각해보겠습니다. 우선 $z$ 로 오는 경로 1 같은 경우 $\Delta y = 0$ 또한 경로 2는 $z$로 아주 가까운 위치만 봐야합니다! 그렇기에 경로 2는 $\Delta x = 0$ 가 됩니다. (그 이유는 미분은 먼 위치가 아니라 가장 가까운 위치에서 고려 해야하기때문이죠) 그럼 아래의 식에 대해 쭉 보시면 이해가 될것입니다.

우선 식1을 보게되면 자명합니다. 미분값을 찾기 위해서죠. 다음으로 $\Delta x$ 와 $\Delta y$를 집어 넣어 식을 다시 전개하게되면 아래 식 2 와 같습니다.

그렇게되고 저희는 두가지 조건에 대해서 고려하여 미분가능한지를 확인할 것입니다.
If) 1번 경로일때 $\Delta y = 0$
우선 $\Delta y$ 를 0으로 만들어서 수식을 다시 써보면 다음과 같습니다.

식 3을 전개해보면 아래와 같이 풀이 할 수 있습니다.

식 4같은 경우 $u_x$ 와 $v_x$는 $u(x,y)$ 에대해 $x$에 대해 round(편미분) 했다고 생각하시면 됩니다. $v(x,y)$ 도 마찬가지 입니다!
If) 2번경로일때 $\Delta x = 0$
$\Delta x$ 를 0으로 만들어서 수식을 다시 써보면 다음과 같습니다.

이 식도 마찬가지로 계산해보면 아래와 같이 나오게됩니다.

이런식으로 전개하여 $f'(z)$를 비교하여 같게 두면 아래와 같이 전개됩니다. 아래 식은 경로 1번에서 나온식입니다.

이 아래식은 경로 2에 의해 나온 수식과 겹쳐 만들면 아래와 같이 됩니다.

이렇듯 코시 리만 부등식에 대해 증명해보았습니다.



